Multivariate Topology

Since about 2012, one of my principal interests has been topological analysis of multiple functions, since real-world simulations in particular rarely generate only one function at a time for a given physical phenomenon.

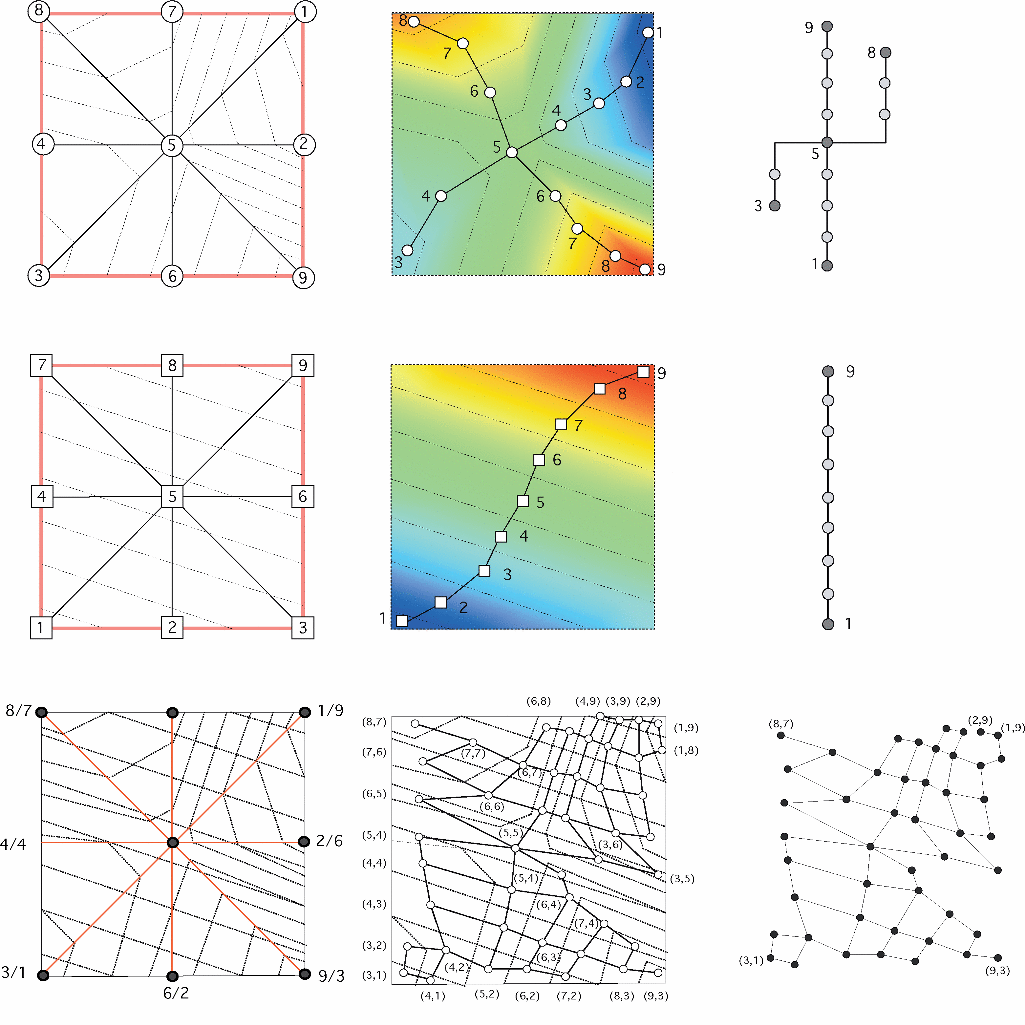
Much of this work was carried out under the META grant (Multifield Extension of Topological Analysis), starting with a quantised approximation we called the Joint Contour Net or JCN (IEEE Visualization 2011 Honorable Mention Poster):

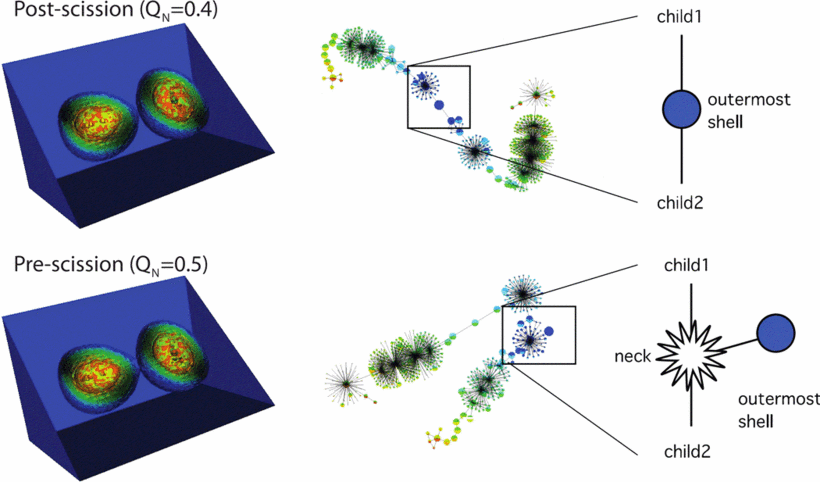
This proved surprisingly effective at analysing a problem in nuclear physics, assisting scientists to better understanding of the process of scission during nuclear fission:

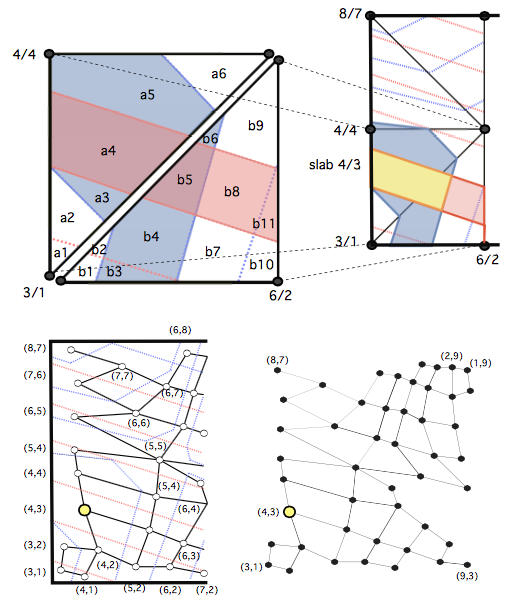
As with scalar topology, simplification rapidly became important, and we explored how to achieve it:

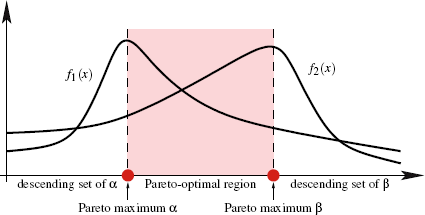
And how it related to the existing field of Pareto analysis:

We exploited the Joint Contour Net to build user interfaces to support mathematicians in studying fiber topology:

Along the way, we experimented with performing the same computation in functional programming languages:

Eventually, we were able to construct an accurate (non-quantised) algorithm for the volumetric bivariate case: (IEEE Visualization 2016 Best Paper Award, ACM Computing Reviews Best of Computing 2016, Also Presented at ACM SIGGRAPH 2017)

A secondary result from this work was some consideration of pathological and test cases for computational topology, including some foldable models of Reeb Spaces:

Multivariate Topology