Skip to main content

MeshingNet

Conference: ICCS 2020: International Conference on Computational Science

Zheyan Zhang, Yongxing Wang, Peter Jimack, He Wang


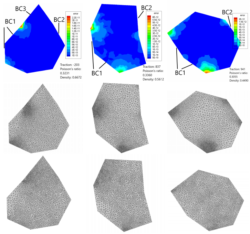
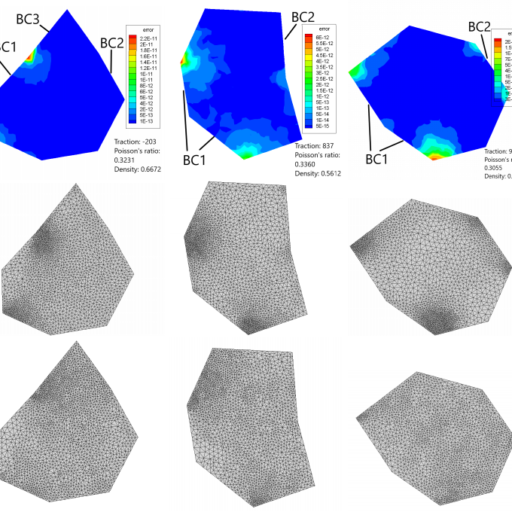
Mesh generation is a critical step for a wide range of computational science problems. This project focus on finite element unstructured meshes. We have been seeking for efficient algorithms to accelerate mesh generation. In particular, deep learning are used as agent to guide mesh generator to produce high quality non-uniform meshes without the cost of error estimation. This paper we use 2d Poisson's equation and linear elasticity problems as test case. Error analysis tells neural networks guided meshes are not only better than uniforms, but even have potential to outperforms meshes generated by conventional error estimators.

Papers

Z. Zhang, P. Jimack, and H. Wang, MeshingNet3D: Efficient generation of adapted tetrahedral meshes for computational mechanics, Advances in Engineering Software, vol. 157-158, 2021.
Abstract | Bibtex | PDF
We describe a new algorithm for the generation of high quality tetrahedral meshes using artificial neural networks. The goal is to generate close-to-optimal meshes in the sense that the error in the computed finite element (FE) solution (for a target system of partial differential equations (PDEs)) is as small as it could be for a prescribed number of nodes or elements in the mesh. In this paper we illustrate and investigate our proposed approach by considering the equations of linear elasticity, solved on a variety of three-dimensional geometries. This class of PDE is selected due to its equivalence to an energy minimization problem, which therefore allows a quantitative measure of the relative accuracy of different meshes (by comparing the energy associated with the respective FE solutions on these meshes). Once the algorithm has been introduced it is evaluated on a variety of test problems, each with its own distinctive features and geometric constraints, in order to demonstrate its effectiveness and computational efficiency.
@article{wrro173988,
volume = {157-158},
month = {July},
author = {Z Zhang and PK Jimack and H Wang},
note = {{\copyright} 2021 Elsevier Ltd. This is an author produced version of an article published in Advances in Engineering Software. Uploaded in accordance with the publisher's self-archiving policy.},
title = {MeshingNet3D: Efficient generation of adapted tetrahedral meshes for computational mechanics},
publisher = {Elsevier},
journal = {Advances in Engineering Software},
year = {2021},
url = {https://eprints.whiterose.ac.uk/173988/},
abstract = {We describe a new algorithm for the generation of high quality tetrahedral meshes using artificial neural networks. The goal is to generate close-to-optimal meshes in the sense that the error in the computed finite element (FE) solution (for a target system of partial differential equations (PDEs)) is as small as it could be for a prescribed number of nodes or elements in the mesh. In this paper we illustrate and investigate our proposed approach by considering the equations of linear elasticity, solved on a variety of three-dimensional geometries. This class of PDE is selected due to its equivalence to an energy minimization problem, which therefore allows a quantitative measure of the relative accuracy of different meshes (by comparing the energy associated with the respective FE solutions on these meshes). Once the algorithm has been introduced it is evaluated on a variety of test problems, each with its own distinctive features and geometric constraints, in order to demonstrate its effectiveness and computational efficiency.}
}
Z. Zhang, Y. Wang, P. Jimack, and H. Wang, MeshingNet: A New Mesh Generation Method based on Deep Learning, Springer Verlag, 2020.
Abstract | Bibtex | PDF
We introduce a novel approach to automatic unstructured mesh generation using machine learning to predict an optimal finite element mesh for a previously unseen problem. The framework that we have developed is based around training an artificial neural network (ANN) to guide standard mesh generation software, based upon a prediction of the required local mesh density throughout the domain. We describe the training regime that is proposed, based upon the use of a posteriori error estimation, and discuss the topologies of the ANNs that we have considered. We then illustrate performance using two standard test problems, a single elliptic partial differential equation (PDE) and a system of PDEs associated with linear elasticity. We demonstrate the effective generation of high quality meshes for arbitrary polygonal geometries and a range of material parameters, using a variety of user-selected error norms.
@misc{wrro159526,
volume = {12139},
month = {June},
author = {Z Zhang and Y Wang and PK Jimack and H Wang},
note = {{\copyright} Springer Nature Switzerland AG 2020. This is an author produced version of a conference paper published inLecture Notes in Computer Science. Uploaded in accordance with the publisher's self-archiving policy.},
booktitle = {ICCS 2020: International Conference on Computational Science},
title = {MeshingNet: A New Mesh Generation Method based on Deep Learning},
publisher = {Springer Verlag},
year = {2020},
journal = {Lecture Notes in Computer Science},
pages = {186--198},
keywords = {Mesh generation; Error equidistribution; Machine learning; Artificial neural networks},
url = {https://eprints.whiterose.ac.uk/159526/},
abstract = {We introduce a novel approach to automatic unstructured mesh generation using machine learning to predict an optimal finite element mesh for a previously unseen problem. The framework that we have developed is based around training an artificial neural network (ANN) to guide standard mesh generation software, based upon a prediction of the required local mesh density throughout the domain. We describe the training regime that is proposed, based upon the use of a posteriori error estimation, and discuss the topologies of the ANNs that we have considered. We then illustrate performance using two standard test problems, a single elliptic partial differential equation (PDE) and a system of PDEs associated with linear elasticity. We demonstrate the effective generation of high quality meshes for arbitrary polygonal geometries and a range of material parameters, using a variety of user-selected error norms.}
}

Authors from VCG

Zheyan Zhang

Zheyan Zhang

phd candidate

He Wang

He Wang

Associate Professor